7.2. Trabajo de prácticas: Divisor serie¶
7.2.1. Objetivos¶
El objetivo general de esta práctica es la realización de un divisor serie y su implementación en la tarjeta DE10-Lite.
El trabajo se realizará individualmente.
7.2.2. Introducción¶
La especificación funcional del divisor serie es la siguiente:
Entradas:
\(x = (x_{n-1}, \cdots x_{1},x_{0}) \; x_i \in \{0,1\}\); \(0 \leq x \leq 2^n - 1\)
\(y = (y_{m-1}, \cdots y_{1},y_{0}) \; y_i \in \{0,1\}\); \(0 \leq y \leq 2^m - 1\)
con \(m \leq n\)
Salidas:
\(q = (q_{n-1}, \cdots q_1, q_0) \; q_k \in \{0,1\}\); \(0 \leq q \leq (2^n - 1)\)
\(r = (r_{m-1}, \cdots r_1, r_0) \; r_k \in \{0,1\}\); \(0 \leq r \leq (2^m - 1)\)
Función:
Para la realización de un divisor serie utilizamos el algoritmo de división básico visto en el colegio, que se puede resumir en el siguiente pseudocódigo:
1. Desplazamos el denominador (y) a la izquierda hasta coincidir en orden de magnitud con el numerador (x).
2. Comparamos el numerador con el denominador desplazado. Extraemos un dígito n del cociente.
3. Actualizamos el numerador restándole n veces el denominador desplazado.
4. Comparamos el denominador con el denominador desplazado:
a. si el denominador desplazado es mayor, lo desplazamos una posición a la derecha y volvemos al paso 2.
b. en caso contrario, devolvemos el cociente y el resto.
Este algoritmo se puede adaptar para trabajar con números binarios, considerando que los anchos del numerador y del denominador son fijos y conocidos de antemano:
i = 4
p_high = 0;
p_low = x_in;
q_temp = 0;
//Iteramos un número de veces igual a n, el ancho en bits del numerador x_in
op : p = p_high & p_low;
p = p << 1;
q_temp = q_temp << 1;
p_high = p[m+n-1:n]; // m es el ancho en bits del denominador y_in
p_low = p [n-1:0];
if (p_high >= y_in) then
{
p_high = p_high - y_in;
q_temp = q_temp + 1;
}
i = i -1;
if (i != 0) then {goto op};
q = q_temp;
r = p_high;
el número de iteraciones es igual al ancho en bits del numerador x. Un ejemplo que resuelve la división de 11/3 sería el siguiente, asumiendo un ancho de 4 bits para x_in e y_in:
Advertencia
Debe añadirse un bit más en p para evitar desbordamiento.
Paso# |
índice |
valor de p, q |
Comentario |
|---|---|---|---|
0 |
i = 0 |
p: 0 0000 1011 q: 0000 |
p se inicializa con el valor de x: (\(p_h = 0 \; p_l = x\))
q se inicializa a 0.
|
1 |
i = 0 |
p: 0 0001 0110 q: 0000 |
\(p \ll 1\) desplaza p a la izquierda (\(p = 2 \cdot p\))
\(p_h < y \Rightarrow\) sin cambios
\(q \ll 1\) desplaza q a la izquierda (\(q = 2 \cdot q\))
|
2 |
i = 1 |
p: 0 0010 1100 q: 0000 |
\(p \ll 1\) desplaza p a la izquierda (\(p = 2 \cdot p\))
\(p_h < y \Rightarrow\) sin cambios
\(q \ll 1\) desplaza q a la izquierda (\(q = 2 \cdot q\))
|
3 |
i = 2 |
p: 0 0101 1000 q: 0000
p: 0 0010 1000 q: 0001
|
\(p \ll 1\) desplaza p a la izquierda (\(p = 2 \cdot p\))
\(p_h > y \Rightarrow p_h = p_h - y\)
\(q \ll 1 + 1\) desplaza q a la izquierda y suma 1 (\(q = 2 \cdot q + 1\))
|
4 |
i = 3 |
p: 0 0101 0000 q: 0010
p: 0 0010 00000 q: 0011
|
\(p \ll 1\) desplaza p a la izquierda (\(p = 2 \cdot p\))
\(p_h > y \Rightarrow p_h = p_h - y\)
\(q \ll 1 + 1\) desplaza q a la izquierda y suma 1 (\(q = 2 \cdot q + 1\))
|
i = 4 |
p: 0010 0000 q: 0011 |
Resultado final (q = 3, r = 2) |
El proceso de división generará tres salidas: el cociente (quotient_out), el resto (reminder_out) y otra salida que indicará que el resultado es incorrecto porque el denominador es cero (NaN, Not a Number).
7.2.3. Esquema general del divisor¶
Antes de realizar la descripción VHDL del divisor serie debe realizarse un esquema con los distintos elementos que lo van a componer. El circuito final estaría constituido por la unidad de control y el data-path, según se muestra en la Figura 7.8.
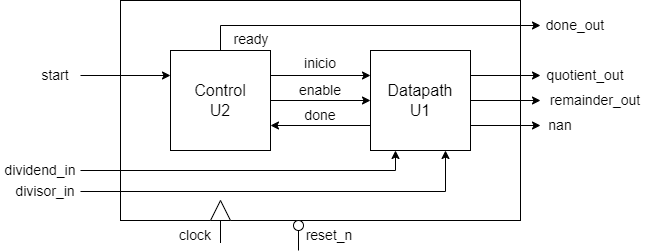
Figura 7.8 Diagrama de bloques del divisor serie con la unidad de control y la unidad de data-path.¶
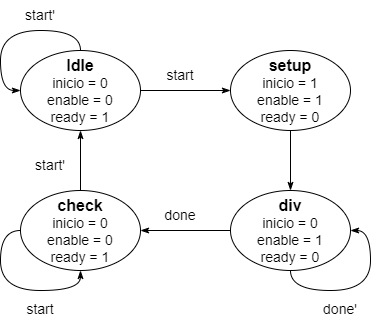
La unidad de control generará dos señales. La señal de inicio indicará que comenzamos la realización de un nuevo producto y la señal de enable activará el proceso de multiplicación, habilitando un contador que hará la función del indice i en el algoritmo de división.
7.2.3.1. Definición del data-path¶
Las operaciones necesarias son una resta (en el caso que \(p_{high} \geq y\) se resta y), una suma (si \(p_{high} \geq y\) se incrementa q_temp en 1) y desplazamientos hacia la izquierda para las señales internas p y q_temp. Sin embargo, la implementación que vamos a hacer de este algoritmo tendrá unos anchos de 8 y 4 bits para x e y respectivamente. La realización de este circuito se hace siguiendo el siguiente diagrama de bloques, que corresponde al data-path del divisor serie:
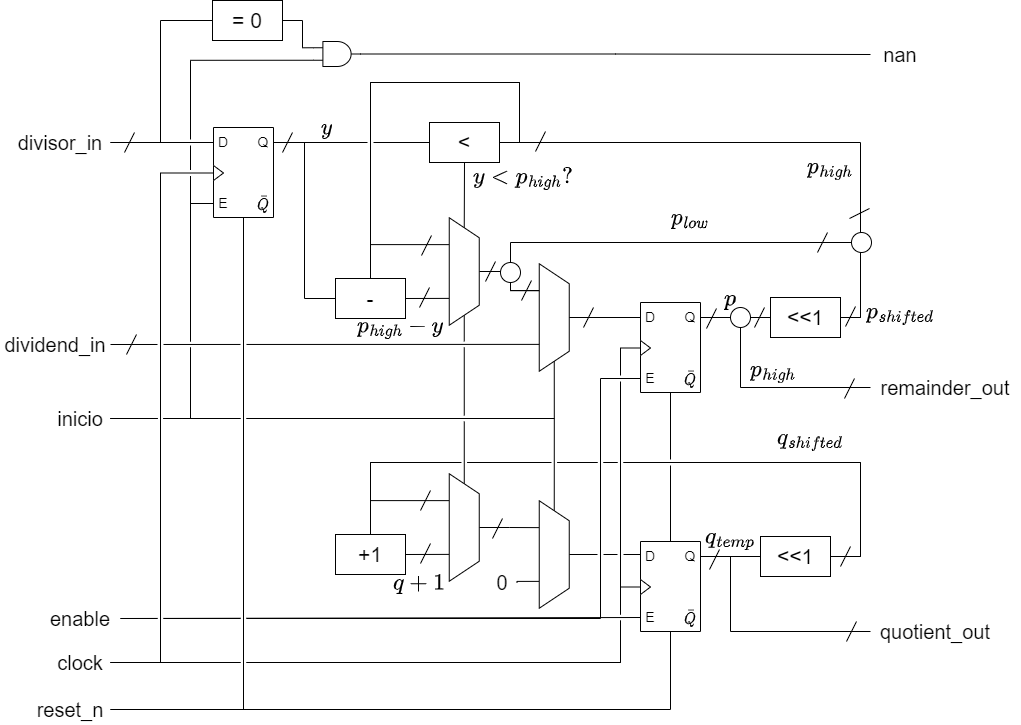
Figura 7.9 Diagrama de bloques del data-path del divisor serie.¶
Los registros mantienen los valores de p y q_temp. Los multiplexores a su entrada se usan para inicializar sus valores, a dividend_in (x) y 0 respectivamente. En cada ciclo de reloj, el contenido de ambos registros se desplaza una posición a la izquierda. Luego, se compara la parte alta de p con la entrada divisor_in (y), que también se registra durante la inicialización. Si se cumple la condición de que \(p_h \geq y\), entonces se actualizan los valores de p y q_temp con las operaciones de resta e incremento en 1, respectivamente. Al finalizar todas las etapas de la división, el registro q_temp almacena el resultado de la división entera, mientras que la parte alta del registro p almacena el resto.
Aparte del funcionamiento normal de este circuito, debemos tener en cuenta un caso especial. La división por 0 es una indeterminación que nos daría un resultado erróneo si seguimos el algoritmo de división planteado. Por ello, se introduce una comparación del divisor con el valor 0 como parte de la inicialización del datapath. En tal caso, se activa un flag de salida adicional indicando la condición de NaN (Not-a-Number) y se omiten el resto de etapas del algoritmo de división.
La descripción VHDL del diseño se va a realizar en VHDL a partir del esquema de la Figura 7.9. A este circuito habrá que añadir un contador (no mostrado en la Figura 7.9) que indicaría el número de ciclos de reloj que necesita este circuito para tener el resultado final. El resultado final (cociente, resto y nan), se almacenará en sendos registros del tamaño adecuado (no mostrados en la Figura 7.9).
7.2.4. Trabajo previo¶
Antes de realizar la descripción VHDL del divisor debe realizarse un esquema con los distintos elementos que lo van a componer. Para la descripción de la máquina de control se utilizará el VPL del Campus Virtual.
7.2.5. Trabajo de laboratorio¶
7.2.5.1. Describir la unidad de data-path en VHDL y y simular con Modelsim-Altera¶
En primer lugar se deberá describir en VHDL el data-path que se representa en la Figura 7.9. Los registros que aparecen en este esquema deben realizarse con el código VHDL del Listado 7.8 (registro de n bits).
Para hacer la descripción del data-path en VHDL se debe realizar el VPL disponible en el Campus Virtual.
7.2.5.2. Implementar la unidad de data-path en QuartusII y simular con Modelsim-Altera¶
Implementar en el QuartusII/Modelsim-Altera la unidad de data-path. Para ello utilizaremos la descripción realizada en el VPL. Se debe crear un proyecto en Quartus y crear un nuevo fichero VHDL para describir la función del data-path del divisor serie e introducir en este fichero la descripción realizada en el VPL descrito en el apartado Describir la unidad de data-path en VHDL y y simular con Modelsim-Altera y guardar el fichero como divisor_datapath.vhd. Para realizar la simulación se debe:
Declarar a divisor_datapath.vhd como el top-level del circuito.
En el data-path se deben incluir un contador de 8 pulsos de reloj que debe realizarse según el código VHDL del Listado 7.9. Añadir a Quartus las descripciones VHDL proporcionadas en el Campus Virtual: registro_enable.vhd (Listado 7.8) y contador_k.vhd (Listado 7.9).
Compilar el diseño y corregir los errores, si los hubiera.
Simular este circuito usando Modelsim-Altera.
Crear un nuevo fichero de formas de onda con el University Wafeform VWF (Waveform.vwf).
Introducir todos los pines del circuito en el diagrama de formas de onda.
Ordenar las señales según se observa en la siguiente figura:
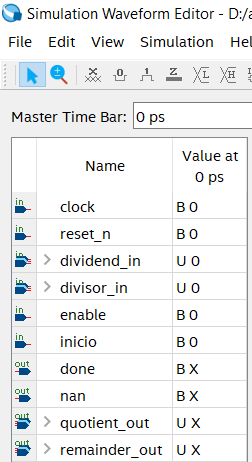
Figura 7.11 Señales para simular el data-path del divisor.¶
Establecer el tiempo de simulación en 1 us (1000 ns).
Seleccionar para las señales dividend_in, divisor_in , quotient_out y remainder_out el radix como “Unsigned Decimal”.
Establecer una señal de reloj de 20 MHz y el resto de las señales tal como aparece en la figura siguiente:

Figura 7.12 Estímulos para simular el data-path del divisor.¶
Realizar la simulación y comprueba que el resultado es el siguiente, donde se observa que al multiplicar 64/7 el resultado es 9, más 1 de resto. Además, comprobamos que se activa el flag de NaN cuando introducimos un valor de 0 en el divisor.

Figura 7.13 Resultados de simulación del data-path del divisor.¶
7.2.5.2.1. Implementar la unidad de control en Quartus¶
En esta sección se realizará la implementación de la máquina de control en Quartus II utilizando la descripción realizada en el VPL descrito en el apartado Definición de la unidad de control y guardarlo con el nombre divisor_control.vhd. Para simularlo seguir los siguientes pasos:
Declarar a divisor_control.vhd como el top-level del circuito.
Establecer como preferencia de Quartus II la codificación Gray.
Seleccionar Assignements > settings > Compiler setting > Advanced setting (Synthesis).
En la casilla “Filter” poner “State”.
En el cuadro “State Machine Processing“ seleccionar “Gray” y aceptar hasta volver a la página principal de Quartus II.
Compilar el diseño y corregir errores si los hubiera.
Crear un nuevo fichero de formas de onda con el University Wafeform VWF (Waveform1.vwf).
Simular este circuito usando Modelsim-Altera.
Introducir todos los pines del circuito en el diagrama de formas de onda.
Ordenar las señales de la siguiente manera: clock, reset_n, start, done, enable, inicio, ready.
Establecer el tiempo de simulación en 800 ns.
Definir el reloj como una señal periódica de 50 ns (20 MHz) y el reset_n siempre a ‘1’ a excepción de los primeros 50 ns que estará a ‘0’.
Añadir las variables de estado: Edit > Insert Node o Bus > Node Finder. En la nueva ventana en la casilla “Filter” seleccionar “All & Registers Post-fitting” y luego seleccionar “List”. Incluir en el diseño en orden a su peso.
En la ventana de formas de ondas seleccionar las variables de estado y agruparlas. El nombre del grupo debe ser “estado”. Mover el grupo justo debajo de la señal done.
Secuencia de entradas siguiente a partir de los 50 ns iniciales.
La asignación de entradas debe ser como indica la figura siguiente:

Figura 7.14 Estímulos para verificar la máquina de control del divisor serie.¶
Ejecutar la simulación en Modelsim-Altera (Simulation > Run Functional Simulation).
Comprobar que los resultados son los esperados según la transparencia la figura siguiente.

Figura 7.15 Resultados de simulación de la máquina de control del divisor serie.¶
7.2.5.2.2. Implementar el divisor serie en Quartus¶
Finalmente se deberá describir estructuralmente el divisor serie como una unidad de control y unidad de data-path conectadas tal como se ve en la Figura 7.8. Se debe crear la descripción del divisor serie siguiendo el esquema de la Figura 7.8 y guardarla descripción con el nombre divisor_top.vhd. Para la descripción usar la entidad tal como se describe en el (Listado 7.10).
7.2.5.2.3. Implementar y validar el multiplicador serie en la tarjeta DE10-Lite¶
Una vez terminado el proceso anterior se proderá a la implementación del diseño en la tarjeta DE_10 Lite. Para ello tendremos los ficheros VHDL necesarios en el Campus Virtual:
TrabajoPR2.vhd que representa la descripción del sistema completo y las conexiones de entrada/salida de la placa DE10-Lite.
Las descripciones proporcionadas en la Práctica 5 (ver Listado 7.8, Listado 7.9, Listado 7.10 y Listado 7.12), también disponibles en el Campus Virtual:
binary_to_7seg_display.vhd, que representa un valor en binario en un display de 7 segmentos;
bynary_to_BCD.vhd y binary_to_bcd_digit.vhd, que convierten un valor binario en código BCD; y
BCD_7segment.vhd, que representa un valor en BDC en un display de 7 segmentos.
La conexión de los pines se muestra en la siguiente Figura:

Figura 7.16 Pin-out de la Práctica 6.¶
Debido a que la tarjeta no tiene suficientes switches, del dividendo se pueden configurar únicamente los 6 bits menos significativos, quedando los otros 2 bits fijos a 0. Por otro lado, en los displays de 7 segmentos los valores correspondientes al dividendo y el cociente se muestran codificados en BCD, mientras que el divisor y el resto se muestran en hexadecimal. En el caso de que se active la salida de NaN, los displays correspondientes a la salida (cociente y resto) mostrarán el valor «nAn».
7.2.6. Entregables¶
7.2.6.1. Trabajo teórico¶
Por hacer
ET2.1. Memoria de trabajo incluyendo el diagrama de ejecución del divisor.
ET2.2. Diagrama de bloques completo del divisor serie.
7.2.6.2. Trabajo práctico¶
Por hacer
ET2.3. Realizar la descripción VHDL funcional del data-path del divisor serie del apartado Describir la unidad de data-path en VHDL y y simular con Modelsim-Altera en el VPL disponible en el Campus Virtual.
ET2.4. Realizar la descripción VHDL de la unidad de control del divisor serie en el VPL disponible en el Campus Virtual.
ET2.5. Implementación del divisor serie en la tarjeta DE10-Lite.
7.2.7. Listados VHDL¶
-- Ver en el campus Virtual de la Asignatura
-- Ver en el campus Virtual de la Asignatura
ENTITY divisor_top IS
PORT(
dividend_in : IN STD_LOGIC_VECTOR(7 DOWNTO 0);
divisor_in : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
start_in : IN STD_LOGIC;
quotient_out : OUT STD_LOGIC_VECTOR(7 DOWNTO 0);
remainder_out : OUT STD_LOGIC_VECTOR(3 downto 0);
done_out : OUT STD_LOGIC;
nan_out : OUT STD_LOGIC;
reset_n : IN STD_LOGIC ;
clock : IN STD_LOGIC);
END divisor_top;
-- Ver en el campus Virtual de la Asignatura
--Electronica Digital 2º curso EITE/ULPGC
--Para usar únicamente en los Trabajos de asignatura
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.numeric_std.all;
USE work.all;
entity divisor_tb is
end divisor_tb;
ARCHITECTURE tb OF divisor_tb IS
COMPONENT divisor_top IS
PORT(
dividend_in : IN STD_LOGIC_VECTOR(7 DOWNTO 0);
divisor_in : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
start_in : IN STD_LOGIC;
quotient_out : OUT STD_LOGIC_VECTOR(7 DOWNTO 0);
remainder_out : OUT STD_LOGIC_VECTOR(3 DOWNTO 0);
nan_out : OUT STD_LOGIC;
done_out : OUT STD_LOGIC;
reset_n : IN STD_LOGIC;
clock : IN STD_LOGIC);
END COMPONENT;
SIGNAL start_in : STD_LOGIC;
SIGNAL dividend_in : STD_LOGIC_VECTOR (7 DOWNTO 0);
SIGNAL divisor_in : STD_LOGIC_VECTOR (3 DOWNTO 0);
SIGNAL clock : STD_LOGIC;
SIGNAL quotient_out : STD_LOGIC_VECTOR (7 DOWNTO 0);
SIGNAL remainder_out : STD_LOGIC_VECTOR (3 DOWNTO 0);
SIGNAL nan_out : STD_LOGIC;
SIGNAL done_out : STD_LOGIC;
SIGNAL reset_n : STD_LOGIC;
SIGNAL TbClock : STD_LOGIC := '0';
SIGNAL TbSimEnded : STD_LOGIC := '0';
CONSTANT TbPeriod : TIME := 40 ns;
BEGIN
dut: divisor_top PORT MAP(
dividend_in => dividend_in,
divisor_in => divisor_in,
start_in => start_in,
quotient_out => quotient_out,
remainder_out => remainder_out,
done_out => done_out,
nan_out => nan_out,
reset_n => reset_n,
clock => clock
);
TbClock <= NOT TbClock AFTER TbPeriod/2 WHEN TbSimEnded /= '1' ELSE '0';
clock <= TbClock;
stimuli : PROCESS
BEGIN
start_in <= '0';
dividend_in <= (others => '0');
divisor_in <= (others => '0');
reset_n <= '1';
WAIT FOR 20 ns;
reset_n <= '0'; -- Se hace un reset del sistema
WAIT FOR 60 ns;
reset_n <= '1';
WAIT FOR 80 ns;
dividend_in <= "01000000"; -- Se hace la división de 64/7
divisor_in <= "0111";
start_in <= '1';
WAIT FOR 10 * TbPeriod;
start_in <= '0';
WAIT FOR 6 * TbPeriod;
dividend_in <= "10000000"; -- Se hace la división de 128/9
divisor_in <= "1001";
start_in <= '1';
WAIT FOR 10 * TbPeriod;
start_in <= '0';
WAIT FOR 6 * TbPeriod;
dividend_in <= "11111111"; -- Se hace la división de 255/15
divisor_in <= "1111";
start_in <= '1';
WAIT FOR 10 * TbPeriod;
start_in <= '0';
WAIT FOR 6 * TbPeriod;
dividend_in <= "00000010"; -- Se hace la división de 2/14
divisor_in <= "1110";
start_in <= '1';
WAIT FOR 10 * TbPeriod;
start_in <= '0';
WAIT FOR 6 * TbPeriod;
dividend_in <= "00001100"; -- Se hace la división de 12/0
divisor_in <= "0000";
start_in <= '1';
WAIT FOR 10 * TbPeriod;
start_in <= '0';
WAIT FOR 6 * TbPeriod;
-- Stop the clock and hence terminate the simulation
TbSimEnded <= '1';
WAIT;
END PROCESS;
END tb;