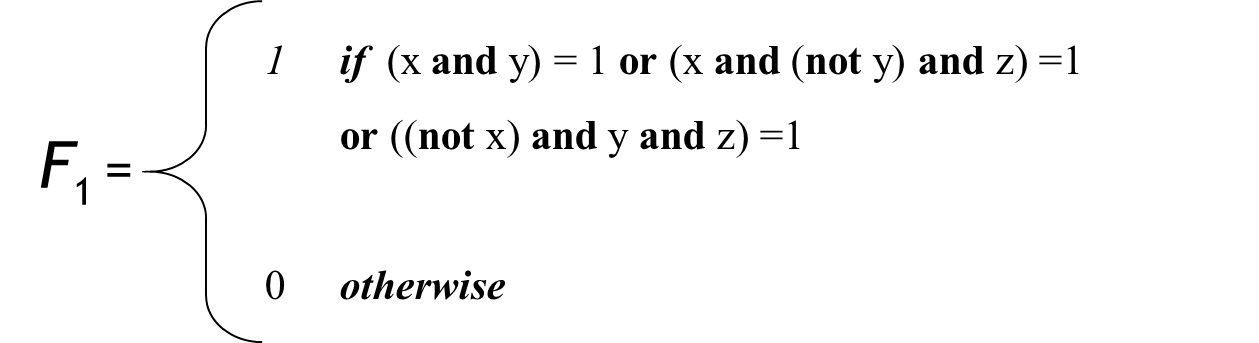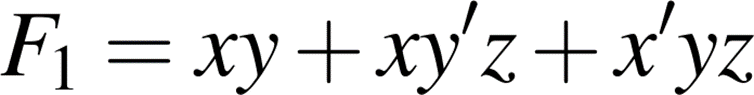3.1.1. Tema 2: Problemas de aula

3.1.1.1. Sistemas numéricos y codificación

1. Convierte el siguiente número octal a hexadecimal y a binario: 637,25 ₈

2. Convierte el siguiente número binario a hexadecimal y a octal: 1100101,0101 ₂

3. Convertir el siguiente número decimal (174,375 ₁₀) a binario, a hexadecimal y a octal.

4. Añadir el bit de paridad par apropiado a los siguientes bytes de datos: 10100100, 00001001 y 11111110

5. A partir del código en binario natural de 3 bits crear:

   1. un código de 4 bits con distancia mínima igual a 2 y

   2. un código Gray de 3 bits:

6. Rellenar la siguiente tabla de conversión de códigos numéricos:

   Código a convertir	Base 2	Base 8	Base 16
   11101010,0101 2	–
   261,367 8		–
   15B,CEF 16			–
   10,6640625 10

3.1.1.2. Algebra de Boole

1. Algebra de conmutación. Indicar cuál de las siguientes transformaciones es verdadera o falsa.

   1. \((W·X + Y^\prime + Z)^\prime = (W^\prime + X^\prime) · Y · Z^\prime\)

   2. \(\sum_{WXYZ}(1,6,11,15) = W^\prime·X^\prime·Y^\prime·Z + W^\prime·X·Y·Z^\prime + W·X^\prime·Y·Z + W·X·Y·Z^\prime\)

2. Demostrar que son ciertas las siguientes expresiones:

   1. \(X·(X^\prime + Y) = X·Y\)

   2. \((X + Y)·(X + Y^\prime) = X\)

   3. \(X·Y·Z·[X·Y + Z^\prime·(Y·Z + X·Z)] = X·Y·Z\)

3.1.1.3. VHDL

1. Realizar la descripción VHDL de la siguiente función f de tres entradas (x, y, z) que viene definida por la siguiente expresión de suma de productos:

   • Especificación funcional:

     • Entradas: \(x, y, z \in \{0, 1\}\).

     • Salida: \(f \in \{0, 1\}\).

     • Función:

   

   • Siguiendo la especificación, la ecuación algebraica de la función es la siguiente:

   

   1. Realizar la tabla de verdad y escribir la expresión en función de sumatorio de minitérminos.

   2. Hacer una descripción VHDL que represente la función.

   3. Hacer un banco de prueba del circuito y probar todas las opciones de la tabla de verdad.