3.1.3. Tema 4: Problemas de aula

3.1.3.1. Análisis de circuitos combinacionales básicos

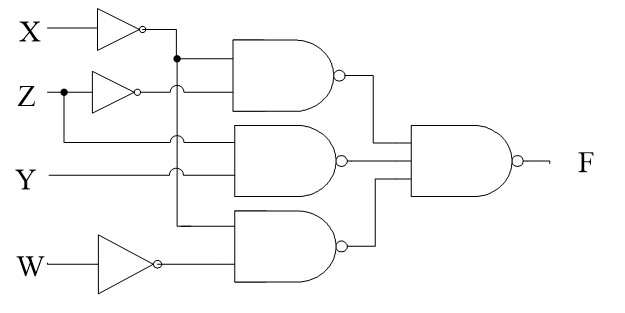
1. Analizar el circuito combinacional siguiente:

   

   y expresar la función F:

   1. Como una tabla de verdad.

   2. Como suma de los minitérminos de cuatro variables.

   3. Como producto de los maxitérminos de cuatro variables.

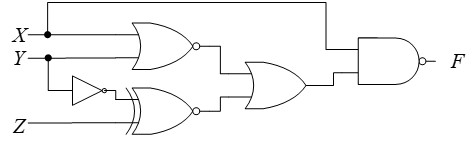
2. Analizar el siguiente circuito en el que las señales tienen el siguiente orden de peso: x, y, z.

   

   1. Escribir la expresión de su salida en función de las entradas.

   2. Escribir la expresión como suma de minitérminos.

   3. Escribir la expresión mínima como suma de productos.

3.1.3.2. Minimización de funciones combinacionales

1. Usando el mapa de Karnaugh:

   1. minimiza la función siguiente usando suma de productos.

      \(F = \sum_{WXYZ}(0,1,2,3,7,8,10,11,15)\)

   2. Usando únicamente puertas NAND y NOT hacer el esquema del circuito.

2. Usando el mapa de Karnaugh:

   1. minimiza la función siguiente usando suma de productos.

      \(F = \sum_{WXYZ}(1, 4, 5, 6, 7, 9, 14,15)\)

   2. Usando únicamente puertas NAND y NOT hacer el esquema del circuito.

3. Usando el mapa de Karnaugh:

   1. minimiza la función siguiente usando suma de productos.

      \(F = \sum_{WXYZ} (2,3,8,9,11,15) + d(0,1,6,10,13)\)

   2. Usando únicamente puertas NAND y NOT hacer el esquema del circuito.

4. Usando el mapa de Karnaugh:

   1. minimiza la función siguiente usando suma de productos.

      \(F = \sum_{WXYZ} (2,3,4,6,12,14) + d(5, 10, 13, 15)\)

   2. Usando únicamente puertas NAND y NOT hacer el esquema del circuito.

5. Usando el mapa de Karnaugh, minimiza la función siguiente usando suma de productos.

   \(F = \sum_{VWXYZ} (5,7,13,15,16,20,25,27,29,31)\)